テキサスホールデムにおいて、抑えておきたい確率を近似的に求めてみます。
但しここで出てくる確率は、あくまで相手のハンドをランダムなものとしますから、実戦では相手のアクションによって相手のハンドレンジを推測し微妙に修正して下さい。(例えば参加率の低いプレイヤーがプリフロップで強いアクションを起こしてきたら、Aを持っている可能性も高いから、自分もAをもっていたら残りのカードにAは2枚しかないだろうとかです。)
2枚のポケットカードがペアになる確率
4C2・13/52C2=1/17 (4種類のスイーツから2つを取る組み合わせ・2~Aまでの数の種類/トランプ52枚から2枚を取る組み合わせ。)
つまり17ハンドに1回はペアができるということです。
ちなみにAAができる確率は1/(17・13)=1/221となります。
これは他の数でも一緒ですが、221ハンドに1回はAAができるということです。
ペアハンドがフロップでセットかフォーカードになる確率
1-48C3/50C3=1-1081/1225=144/1225≒0.11755 (ペアの数字と同じ数を引かない確率の余事象を求めます。)
つまり近似的に考え、ペアハンドでフロップを見に行った時、9回に1回はセットができるということになります。
2枚のカードが同じスーツでフロップでフラッシュドローかフラッシュができる確率
(11C3+11C2・39)/50C3=33/392≒0.0842
約8.4%で大体12回に1回ということになります。
思った程確率は高くなく、毎回同じスーツなら参加するのも考えものだというのが分かります。
2枚のカードが同じスーツでフロップにそのスーツが2枚出た時、ターンかリバーでフラッシュができる確率
1-38C2/47C2=1-703/1081=378/1081≒0.35 (フラッシュにならない確率の余事象を求めます。)
つまり近似的に考え、3回に1回はフラッシュドローを引かれてしまうことになります。
ターンかリバーでオープンエンドストレートドローの引ける確率
1-39/47・38/46=680/2162≒0.3145 (ストレートにならない確率の余事象を求めます。)
引ける確率はフラッシュドローよりも低くなり、3~4回に1回となります。
補足ですがアウツと勝率の関係はターンとリバーでそれぞれ、2倍の法則、4倍の法則で近似的に求まります。
例えばフロップでフラッシュドローをヒットさせたとして、アウツは9枚あります。
フラッシュが完成する確率はターンでは18%、リバーでは36%と見積もることが可能です。
上位のペアハンドが下位のペアハンドにプリフロップでオールインして勝つ確率
46C5/48C5=903/1128≒0.8 (近似的に下位のペアがセットかフォーカードにならない確率としました。)
つまり上位ペアは下位ペアに5回に4回は勝てるということです。逆の見方をすると5回に1回は負けてしまうことになります。
AKハンドがAK以外のペアハンドに対してプリフロップでオールインして勝つ確率
| 5 Σ6Ca・40C5-a/48C5=712746/1712304≒0.416 a=1 |
(近似的にAかKが1枚以上出てAK以外のペアハンドがセットかフォーカードにならない確率としました。)
つまりAKでオールインした場合、AK以外のペアには40%以上の勝率があるということです。
AXハンド(XはA以外)を持っていて、フロップ以降Aが落ちる確率
1-47C5/50C5=1-1419/1960=541/1960≒0.276 (フロップ以降Aが落ちない確率の余事象としました。)
つまり4回に1回以上はAが落ちることになります。
具体的なプリフロップオールイン確率(Card playerで求める)
K♣、K♦対A♦、Q♦
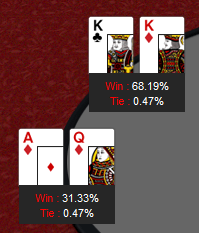
近似的にA♦、Q♦も、3回に1回くらいは勝てるみたいです。